Основи теорії графів

Пропоную навчальні презентації для опрацювання теоретичного матеріалу та виконання практичних завдань

Основні поняття теорії графів. Способи представлення графів. Пошук  у ширину та глибину

Теорія графів — розділ математики, що дає змогу формалізувати взаємозв'язки між різноманітними видами інформації, організувати абстрактне їх представлення.
Графом називається сукупність точок (вершин) і ліній (ребер), що їх з'єднують.

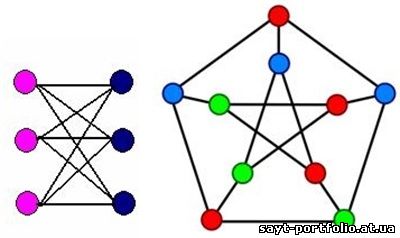
Якщо ребро з'єднує дві вершини, то кажуть, що воно інцидентне цим вершинам, а вершини, які з'єднані таким ребром, називають суміжним.

Якщо кінці ребра належать одній вершині, то таке ребро називається петлею.

Вершини, які не належать кінцям жодного з ребер у графі, називаються ізольованими.

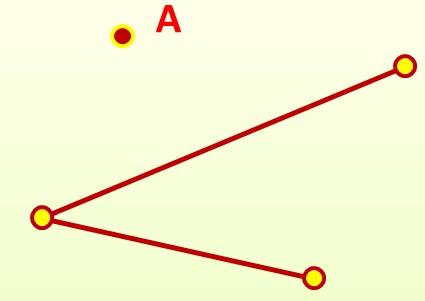
Вершина А – приклад ізольованої вершини.
Граф, який складається лише з ізольованих вершин, називається нуль-графом.

В графі ребро без вершин існувати не може.
Граф називається порожнім, якщо він не має ребер.
Граф, у якому будь-яка пара вершин з'єднана ребрами, називається повним.

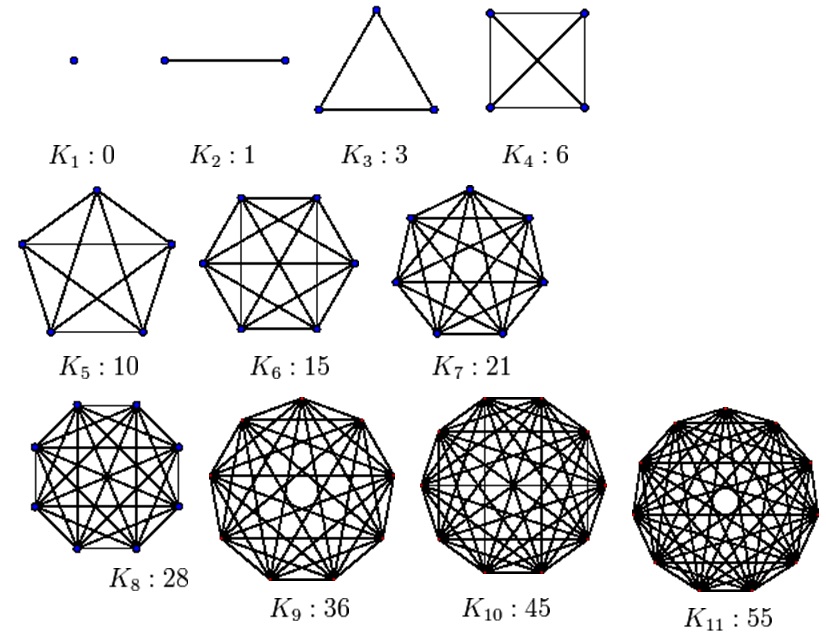
Властивості
Повний граф з n вершинами має n(n - 1)/ 2 ребер
Повний граф з n вершинами є регулярним графом степеня n - 1.
Графи K1 — K4 є планарними. Повні графи з більшою кількістю вершин не є планарними, оскільки містять підграф K5 і, отже, не задовольняють умови Куратовського.
Природно виникає питання: скільки є різних графів з множиною вершин Х, якщо N(X)=n. 
Теорема. Число усіх різних графів з n вершинами дорівнює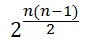 
Якщо всі вершини і ребра графа знаходяться в одній площині, то він називається плоским, у протилежному випадку – просторовим.

  
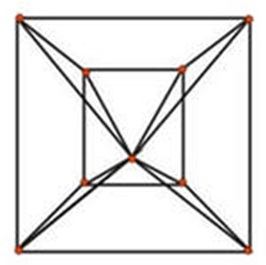
Степенем вершини будемо називати число ребер, яким належить ця вершина. Позначається степінь вершини а як Р(а).
Наприклад,вершина А має степінь 3, а вершина В  - степінь 1: Р(А)=3; Р(В)=1. 

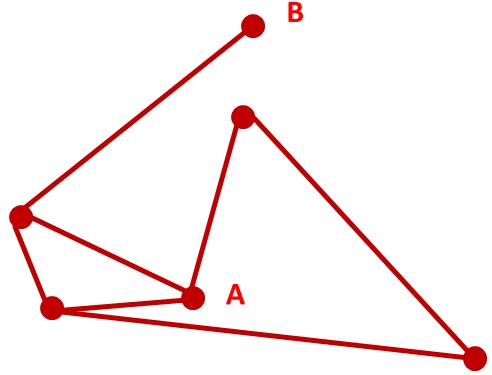
Степенем вершини xi графа називається число вершин xj, які інцидентні вершині xi (число відрізків які виходять з вершини xi).
 Якщо степінь вершини дорівнює 1, то вершина  називається кінцевою вершиною графа. 

Якщо степінь вершини дорівнює 0, то вершини  називається ізольованою.
Нехай задано граф з N вершинами, х1, х2, …, хN. Кажуть, що існує шлях від вершини хi до вершини хj, якщо існує послідовність ребер, яка з'єднує вершини хi і хj. У свою чергу вершини хi та хj є зв'язними, якщо існує шлях від хi до хj.

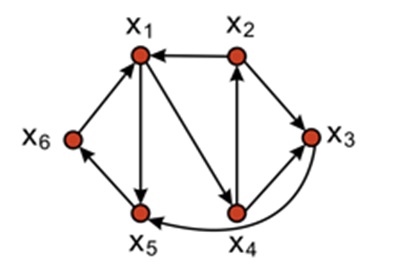
Зв'язні вершини

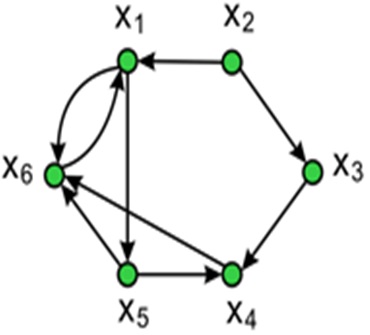
Незв'язні вершини

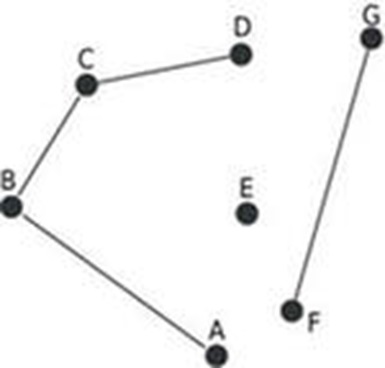
Граф називатимемо зв'язним, якщо будь-яка його вершина зв'язна. 
Повний граф завжди зв'язний, але не всякий зв'язний граф є повним.

 
Циклом називається шлях, в якому збігаються початкова та кінцева вершини. 
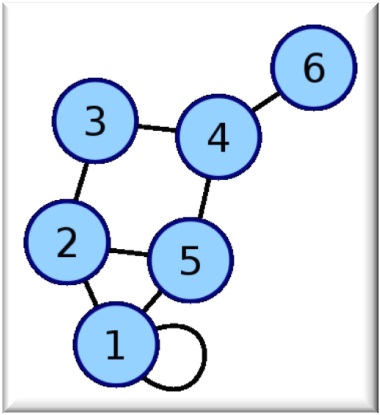
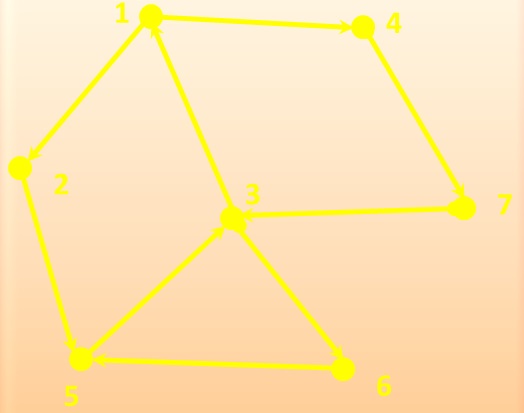
На малюнку зображено граф, який для кожної вершини має по кілька циклів. Наприклад, для вершини 1 існує 6 циклів: (1-2, 2-5, 5-3, 3-1), (1-3, 3-7, 7-4, 4-1), (1-3, 3-5, 5-6, 6-3, 3-1), (1-2, 2-5, 5-6, 6-3, 3-1), (1-2, 2-5, 5-6, 6-3, 3-7, 7-4, 4-1), (1-3, 3-5, 5-6, 6-3, 3-7, 7-4, 4-1).

Якщо цикл через кожну вершину проходить лише один раз, то такий шлях називається простим.
З малюнку видно, що для вершини 1 існує 4 простих цикли: 
1). (1-2, 2-5, 5-3, 3-1), 
2). (1-3, 3-7, 7-4, 4-1), 
3). (1-2, 2-5, 5-6, 6-3, 3-1), 
4). (1-2, 2-5, 5-6, 6-3, 3-7, 7-4, 4-1).
Довжиною шляху (циклу) називається кількість ребер цього шляху (циклу).
Граф, який немає жодного циклу, називається деревом.

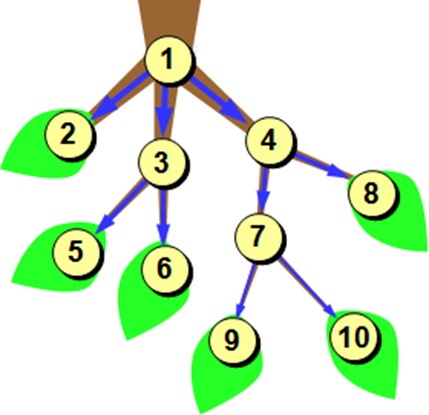
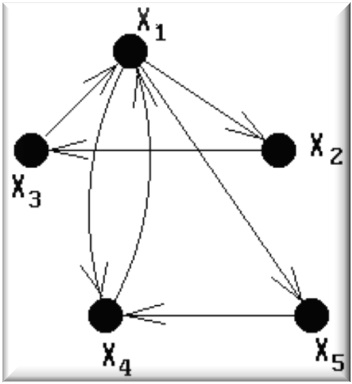
Граф, у якому для всіх ребер вказано напрям, називається орієнтованим, або орграфом.
В орієнтованому графі для вершини 1 існує тільки два орієнтовані цикли:
1). (1-2, 2-5, 5-3, 3-1), 
2). (1-4, 4-7, 7-3, 3-1).

Неорієнтований граф (неограф) — це граф, для кожного ребра якого несуттєвий порядок двох його кінцевих вершин

Для орієнтованих графів специфічним є визначення степенів вершин. 
Для кожної з них окремо визначається вхідний степінь, що дорівнює кількості ребер, які входять у вершину і вихідний степінь, що визначається кількістю ребер, які виходять із неї.
 Сума вхідного і вихідного степенів вершини орієнтованого графа називається степенем цієї вершини.
Орієнтований граф (орграф) — це граф, для кожного ребра якого істотний порядок двох його кінцевих вершин.

 
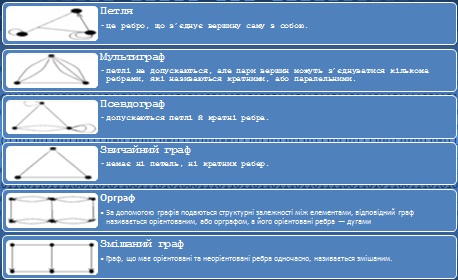
Залежно від типу ребер відрізняють типи графів.

Якщо у графі вказана “вага” кожного ребра, то такий граф називається зваженим.

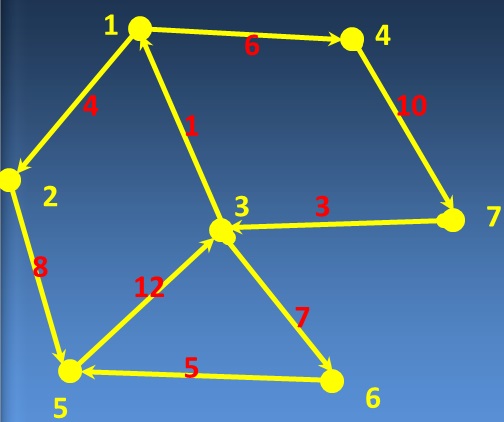
Існують неорієнтовані зважені графи та орієнтовані зважені графи.
Змішаний граф – це граф, що містить як орієнтовані, так і неорієнтовані ребра. Кожен з перерахованих видів графа може містити одне або кілька ребер, у яких обидва кінці сходяться в одній вершині, такі ребра називаються петлями. 
Змішаний граф

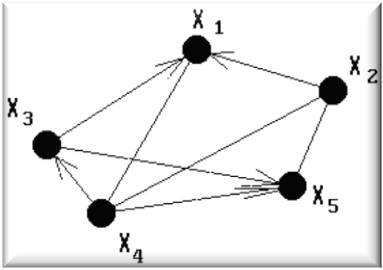
Змішаний граф з петлями

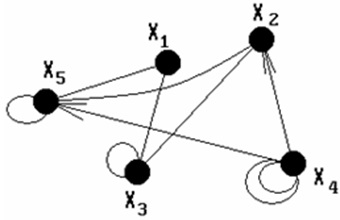
У загальному випадку множина ребер може складатися із трьох непересічних підмножин: підмножини ланок, підмножини дуг і підмножини петель

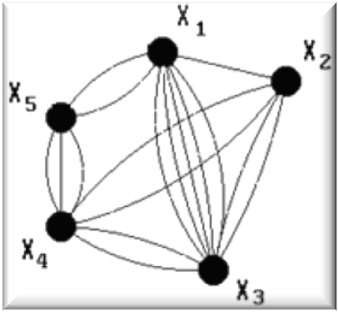
Наочно граф можна уявляти як геометричну конфігурацію, яка складається з точок (вершин графу 1,2,3,4,5,6) і ребер (ліній або відрізків №1(1-3), №2(3-4), №3(4-5), №4(3-5), №5(2-3), №6(2-5), №7(5-6), №8(6-2), №9(2-1), які сполучають деякі точки (вершини) за вибраним алгоритмом 

Сутність геометричної конфігурації графа, в якому всі вершини можна обійти за маршрутом без перетинання ребер графу

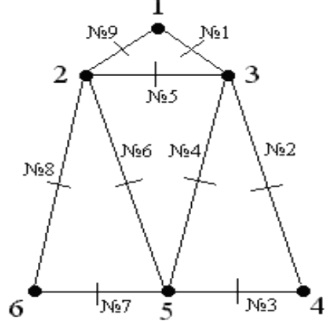
Граф називається ейлеровим, якщо в ньому можна повернутися у ту саму вершину, з якої ми вийшли, обійшовши кожне з ребер тільки один раз.
Схема мостів в Кенігзберзі 

 
Для рішення серйозних математичних задач математик  Ойлер (Euler) використовував наочні ломиголовки.

Одна з них поклала початок зовсім новій області досліджень, що виросла згодом у самостійний розділ математики - теорію графів і топологію. 
Особливість цієї теорії - у геометричному підході до вивчення об'єктів. 
Теорія графів – одна з небагатьох математичних дисциплін, дата народження якої може бути встановлена абсолютно точно.
Перша робота з теорії графів належить Леонарду Ойлеру. Вона з’явилась в публикаціях Санкт-Петербургзської Академії наук у 1736 році.

Праця Ойлера розпочиналася з розгляду однієї ломиголовки так званої „задачі про кенігзберзькі мости”
Сім мостів Кеніґсберґа — видатна історична задача з математики.  Доведення неможливості її розв'язання Леонардом Ейлером в 1735 призвело до створення теорії графів і передувало ідеї топології.
Місто Кенігзберг (нині Калінінград) розташоване на берегах річки Прегель і двох островах. Різні частини міста сполучені сімома мостами. Щонеділі жителі міста любили здійснювати прогулянки по місту. Ойлер поставив питання: чи можна здійснити прогулянку, вийшовши з дому і повернувшись до нього, таку, щоб по кожному мосту пройти рівно один раз.
Формалізуємо задачу про мости.
Схематична карта міста зображена на рисунку 1.

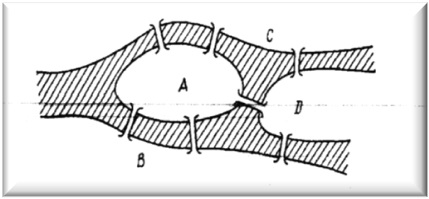
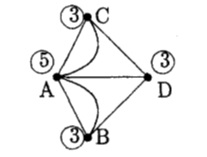 Граф «Кенігзберзьких мостів» в ломиголовці Ойлера.
Чотири частини міста зображені літерами  Оскільки нас цікавлять лише переходи через мости, ми можемо вважати  вершинами графа, ребра якого відповідають мостам. Цей граф зображено на рисунку 2.
Ойлер зауважив, що його граф не являє єдиного циклу: з якої б вершини ми не почали б обхід, ми не можемо обійти весь граф і повернутись назад, не проходячи жодного ребра двічі. Якби такий цикл існував, то з кожної вершини виходило б стільки ребер , скільки в неї входить , інакше кажучи степінь кожної вершини була б парним числом. Таким чином, відповідь на питання Ойлера - негативна.
Виклавши розв'язання задачі про кенігсберзькі мости, Ойлер в своїй праці поставив питання: на яких графах можна знайти цикл, який містить всі ребра графа, при чому кожне ребро зустрічається в циклі рівно один раз?
Це дало початок системному математичному підходу до побудови та вивчення властивості графів.

Зв’язний граф називається ойлеровим графом, якщо існує замкнений ланцюг, який проходить через кожне ребро.
Такий ланцюг називають ойлеровим ланцюгом, або ойлеровим циклом.

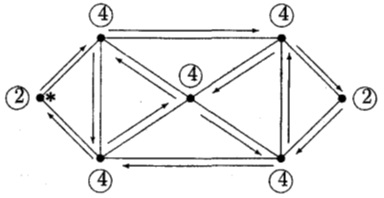
Структура вершин та ребер в неорієнтованому ойлеровому графі (* - означено точку входу ойлерового ланцюга - циклу)
В теорії графів, ейлерів ланцюг — ланцюг в графі, що проходить кожне ребро рівно один раз. Схожим чином, ейлерів цикл — ейлерів ланцюг, що починається і завершується в одній вершині. Вперше розглянуті Леонардом Ейлером під час розв'язання відомої задачі кенігсберзьких мостів в 1736. Математично задача звучить так:
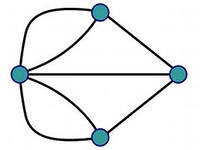
Чи можливо, для графа на малюнку праворуч, побудувати ланцюг (або цикл), що проходить кожне ребро рівно однин раз?
Ейлер довів, що необхідною умовою існування ейлерова циклу є парність степеня кожної вершини графа, і ствердив без доведення, що зв'язний граф з усіма вершинами з парними степенями має ейлерів цикл. Перше повне доведення цього твердження в 1873 оприлюднив Карл Гьєхолзер
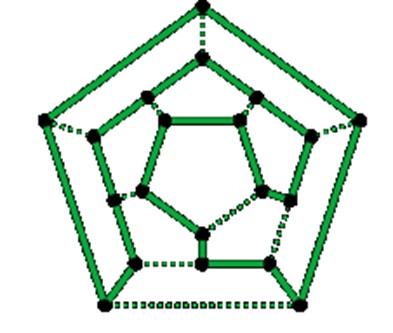
Граф називається гамільтоновим, якщо у ньому можна повернутися у ту саму вершину, з якої ми вийшли, обійшовши кожну з вершин тільки один раз.

Назва гамільтонів граф виникла у зв'язку з тим , що в 1859 році відомий ірландський математик сер Вільям Гамільтон випустив до продажу своєрідну іграшкову головоломку