Тема 3: «Елементи обчислювальної геометрії», 8 годин
Повторення основних понять мови програмування C# (режим форми)
Найпростіші геометричні фігури, їх представлення та властивості
Опрацювати навчальну презентацію з теми
профільна інформатика 11 клас Обчислювальна геометрія 1 урок
Навчальна презентація до уроку. Інструктивний матеріал для практичної роботи
Обчислювальна геометрія. Частина 2. Навчальна презентація до уроку
Лабораторна робота: «Побудова опуклої оболонки».
Тренувальні вправи
1. За даними координатами початку і кінця відрізка знайти довжину відрізка, координати середини даного відрізка.
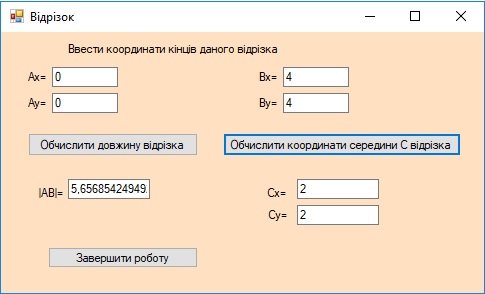
Програмний код
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace WindowsFormsApplication2
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
double x1, y1,x2,y2, d;
x1 = double.Parse(textBox1.Text);
x2 = double.Parse(textBox3.Text);
y1 = double.Parse(textBox2.Text);
y2 = double.Parse(textBox4.Text);
d = Math.Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
textBox5.Text = d.ToString();
}
private void button2_Click(object sender, EventArgs e)
{
double x1, y1, x2, y2, xc, yc;
x1 = double.Parse(textBox1.Text);
x2 = double.Parse(textBox3.Text);
y1 = double.Parse(textBox2.Text);
y2 = double.Parse(textBox4.Text);
xc=(x2-x1)/2;
yc=(y2-y1)/2;
textBox6.Text = xc.ToString();
textBox7.Text = yc.ToString();
}
private void button3_Click(object sender, EventArgs e)
{
Close();
}
}
}
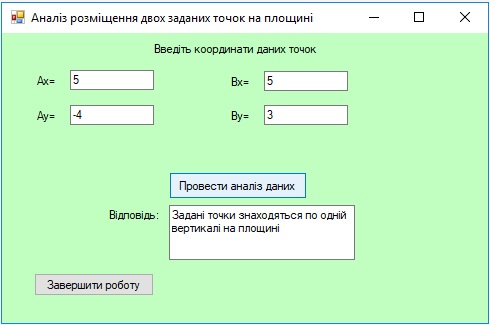
2. За введеними координатами двох точок написати рівняння прямої та розглянути можливі часткові випадки розміщення цієї прямої. (переглянути зразок форми та програмного коду)
Про взаємне розміщення двох точок (x1; y1) і (х2; y2) можна говорити для таких випадків:
- Якщо x1 = x2 і y1 != y2, то задані точки знаходяться по одній вертикалі на площині
- Якщо x1 != x2 і y1 = y2, то задані точки знаходяться по одній горизонталі на площині
- Якщо x1 = x2 і y1 == y2, то задані точки збігаються інакше задані точки не збігаються і не знаходяться по одній вертикалі або горизонталі на площині.
3. За дпними координатами двох точок дослідити їх взаємне розміщення на площині.
private void button1_Click(object sender, EventArgs e)
{
double x1, y1, x2, y2, d;
x1 = double.Parse(textBox1.Text);
x2 = double.Parse(textBox3.Text);
y1 = double.Parse(textBox2.Text);
y2 = double.Parse(textBox4.Text);
if ((x1 == x2) && (y1 != y2))
textBox5.Text = "Задані точки знаходяться по одній вертикалі на площині";
if ((x1 != x2) && (y1 == y2))
textBox5.Text = "Задані точки знаходяться по одній горизонталі на площині";
if ((x1 == x2) && (y1 == y2))
textBox5.Text = "Задані точки збігаються";
if ((x1 != x2) && (y1 != y2))
textBox5.Text = "Задані точки не збігаються і не знаходяться по одній вертикалі або горизонталі на площині";
}
4. Дослідити випадки взаємного розміщення прямої та двох даних точок
Рекомендації.
Нехай задана пряма загальним рівнянням ах + by + с = 0 та дві точки (x1; y1) і (х2; y2). Ознакою того, що точка (х0; у0) лежить на прямій, є ах0 + bуо + с =0. Якщо точка не лежить на прямій, то зрозуміло, що ах0 + bуо + с 0. А це означає, що значення ах0 + bу0 + с або додатне, або від'ємне. Оскільки пряма ах0 + bу0 + с = 0 ділить координатну площину на дві півплощини, то виявляється, що всі точки (xi; yi), які лежать одній з них, дають однаковий знак виразу ах0 + bу0 + с.
Таким чином, можна підбити підсумок наведених міркувань.
Якщо для двох заданих точок (x1; y1) і (х2; y2) має місце вираз (ах1 + bу1 + с)(ах2 + bу2 + с)>0, то це означатиме, що ці дві точки лежать по один бік від заданої прямої ах + by+с=0, а якщо (ах1 + bу1 + с)(ах2 + bу2 + с)< 0, то по різні.

private void button1_Click(object sender, EventArgs e)
{
double a, b, c, x1, y1, x2, y2;
a = double.Parse(textBox1.Text);
b = double.Parse(textBox2.Text);
c = double.Parse(textBox3.Text);
x1 = double.Parse(textBox4.Text);
y1 = double.Parse(textBox5.Text);
x2 = double.Parse(textBox6.Text);
y2 = double.Parse(textBox7.Text);
double z1=(a*x1+b*y1+c)*(a*x2+b*y2+c);
if (z1 > 0) textBox8.Text = "Двi данi точки лежать по один бiк вiд заданоi прямоi ах + by + с = 0";
if (z1 == 0) textBox8.Text = "Обидві точки лежать на даній прямій ах + by+с=0";
if (z1 < 0) textBox8.Text = "Двi данi точки лежать по різні сторони вiд заданоi прямоi ах + by + с = 0";
if (a*x1+b*y1+c==0) textBox8.Text = "Точка M належить заданій прямій";
if (a * x2 + b * y2 + c == 0) textBox8.Text = "Точка N належить заданій прямій";
}
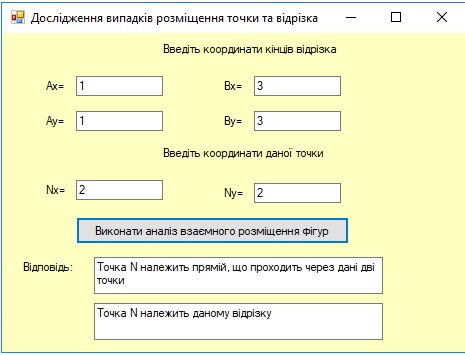
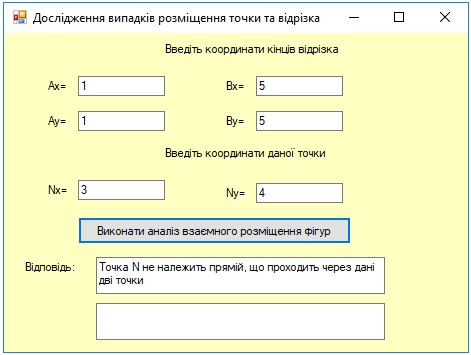
Самостійне виконання дослідження взаємного розміщення точки та відрізка, що задані відповідними координатами.
Рекомендації:
Нехай задана деяка точка (X; Y) і відрізок прямої з координатами своїх кінців (x1; y1) і (х2; y2). Аналіз взаємного розміщення точки і відрізка полягає в отриманні відповіді на запитання: чи належить точка заданому відрізку? Позитивну відповідь можна отримати лише за наявності виконання таких двох умов:
1). Задана точка (X; Y) належить прямій, що проходить через точки (x1; y1) і (х2; y2);
Рівняння прямої (x - x1) (y2 - y1) - (y - y1) (x2 - x1) = 0.
2). Координати точки (X; Y) належать діапазону, що визначається відповідними координатами кінців заданого відрізка.

Тема “Точка і пряма. Рівняння прямої. Коло”
Навчальна презентація до уроку. Завдання для практичного опрацювання теми
Обчислювальга геометрія Точка і пряма Коло
Завдання 1. Пряма проходить через дві задані точки. Знайти кутовий коефіцієнт цієї прямої

private void button1_Click(object sender, EventArgs e)
{
double x1, y1, x2, y2, k;
x1 = double.Parse(textBox1.Text);
y1 = double.Parse(textBox2.Text);
x2 = double.Parse(textBox3.Text);
y2 = double.Parse(textBox4.Text);
k = (y2 - y1) / (x2 - x1);
textBox5.Text = k.ToString();
}
Задача 2. Записати рівняння прямої у загальному вигляді, якщо задано точки, через які ця пряма проходить
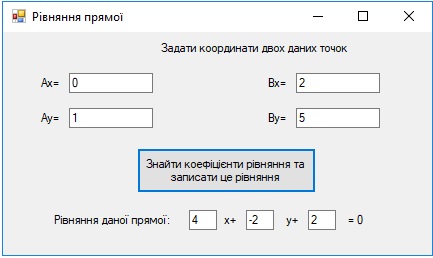
double x1, y1, x2, y2, a,b,c;
x1 = double.Parse(textBox1.Text);
y1 = double.Parse(textBox2.Text);
x2 = double.Parse(textBox3.Text);
y2 = double.Parse(textBox4.Text);
a = y2 - y1;
b = x1 - x2;
c = y1 * x2 - x1 * y2;
textBox5.Text = a.ToString();
textBox6.Text = b.ToString();
textBox7.Text = c.ToString();
Завдання 3. Дано три точки. Перевірити, чи належать ці точки одній прямій.
Для визначення чи розміщені три дані точки (x1; y1), (х2; y2) і (x3; y3) на одній прямій скористайтеся рівнянням прямої (x3-x1)(y2-y1)-(y3-y1)(x2-x1)=0
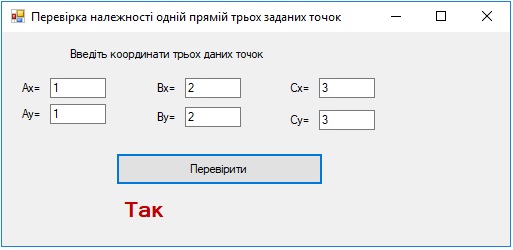
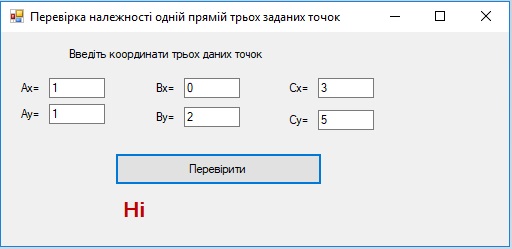
double x1, y1, x2, y2, x3,y3;
x1 = double.Parse(textBox1.Text);
y1 = double.Parse(textBox2.Text);
x2 = double.Parse(textBox3.Text);
y2 = double.Parse(textBox4.Text);
x3 = double.Parse(textBox5.Text);
y3 = double.Parse(textBox6.Text);
if ((x3 - x1) * (y2 - y1) - (y3 - y1) * (x2 - x1) == 0)
label8.Text = "Так";
else
label8.Text = "Ні";
Завдання 4. Дослідити положення даної прямої на координатній площині.
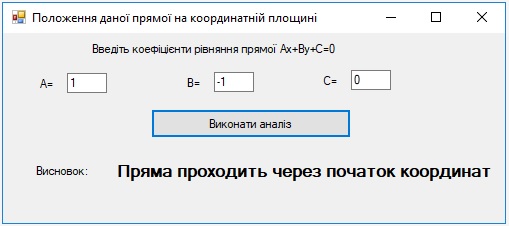
double a, b, c;
a = double.Parse(textBox1.Text);
b = double.Parse(textBox2.Text);
c = double.Parse(textBox3.Text);
if (c == 0) label6.Text = "Пряма проходить через початок координат";
if (a != 0 && b == 0 && c != 0) label6.Text = "Пряма паралельнa осі OY";
if (a != 0 && b == 0 && c == 0) label6.Text = "Пряма - вісь OY";
if (a == 0 && b != 0 && c != 0) label6.Text = "Пряма паралельнa осі OXY";
if (a == 0 && b != 0 && c == 0) label6.Text = "Пряма - вісь OX";
Завдання 5. Знайти тангенс кута між прямими (через кутові коефіцієнти).
double k1, k2, tg;
k1 = double.Parse(textBox1.Text);
k2 = double.Parse(textBox2.Text);
tg=(k2-k1)/(1-k1*k2);
textBox3.Text = tg.ToString();
Самостійне виконання завдань
Опрацювати теоретичних матеріал навчальної презентації та скористатися необхідними співвідношеннями для розв'язання поставлених завдань.
Завдання 6. Знайти кут між прямими, що задані точками, через які прямі проходять.
Рекомендації:
Рівняння прямої, що проходить через 2 дані точки має кутовий коефіцієнт k = (y2 - y1) / (x2 - x1). Далі, див. попередню задачу
Завдання 7. Знайти координати точки, що ділить даний відрізок у заданому відношенні.
Завдання 8. Дослідити випадки взаємного розміщення двох даних прямих
Завдання 9. Знайти координати точки перетину даних прямих
Завдання 10. Перевірити, чи перпендикулярні дані прямі. Розглянути два випадки: через кутові коефіцієнти та через коефіцієнти загального рівняння прямої.
Творче завдання
Завдання 11. Сформулювати 3 різні задачі (за матеріалом 18 слайду навчальної презентації) та провести відповідні дослідження за їх умовами.